Beat the Streak Day Fourteen: Singlearity

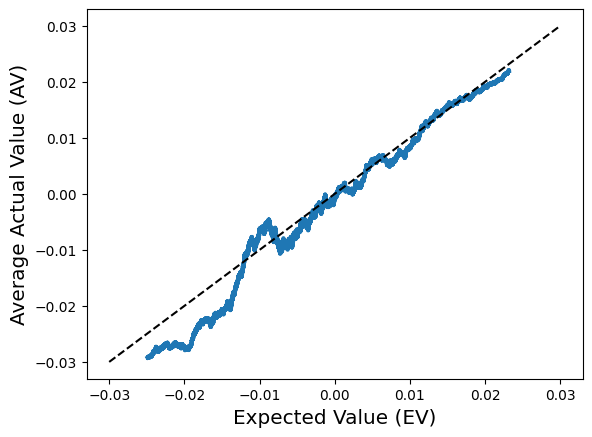
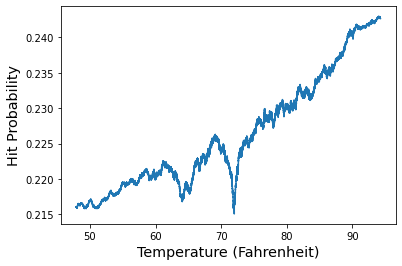
After a fortnight of work, I am back with another blog post on MLBs beat the streak contest. And before you ask, yes that is still a thing in 2023. No one has won it yet, and this year the longest streak was 44, 13 shy of of the number needed and 7 short of the previous all time leader in BTS. In short, it doesn't seem like we're any closer to winning it now than we were 10 years ago. In the last few days, I have been thinking about new algorithms, models, and approaches to this longstanding problem. But before I can or should test these new approaches, it's important to better understand the limitations of simpler approaches when done very carefully. Singlearity was the first approach to this problem I've seen that convincingly demonstrated solid performance where it matters. The idea is to apply standard neural network training techniques on a dataset of (batter, game, outcome) data. The neural network is trained on carefully feature engineered data. Specif...