Ryan's Repository of Random Reflections

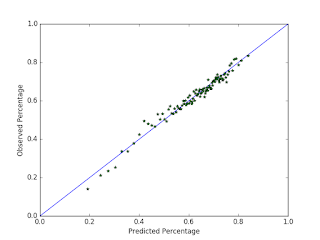
Today I'm going to talk about an interesting game that I thought of, and in particular I'll show the probability that each player will win.  While the rules of the game are not fair, the skill levels of each player are not necessarily the same either, so I formally define what I mean and find the conditions under which these factors balance out.  Without further ado, here is the problem statement: Alice and Bob play a game consisting of an indeterminate number of rounds.  In each round, Alice and Bob compete to win the round, and thus score a point.  Alice is more skilled at this game and so she wins each round with probability $ p > 0.5 $ (independent of the score and other context), meaning Bob wins each round with probability $ 1 - p $.  The score starts at $ 0 - 0 $ and Bob wins if he ever  has more points than Alice, and Alice wins otherwise.  What is the probability that Bob wins this game?  For what value of $ p $ is this game fair? W...

Racket is a derivative of Lisp, and it was also the language used in my first computer science class in college.  It is a functional language which encourages thinking in terms of composing simple functions to accomplish possibly complex goals.  When I was a lab assistant for the class, I recall having a conversation with the professor about how to shuffle a list of numbers in the language, and I came up with an interesting solution which I will talk about in this post. In Racket, you can sort a list of anything by calling the sort function along with a list, and a function to compare any two items in the list.  An example use is (sort (list 4 1 3 2) <) which produces (list 1 2 3 4) .  Since shuffling isn't natively supported in Racket and the simplest shuffling algorithms are not suitable for functional languages with lists instead of arrays, we have to be creative to achieve shuffling behavior.  My idea to shuffle a list was simple: replace the function ...

A decent portion of my blog posts are about mathematical puzzles -- and in particular probability problems.  Unfortunately, since most of the traffic to this blog comes from google searches, those posts don't get nearly as many viewers as some of my other posts.   In order to increase viewership to my other content, I am creating this post to act as a central location where I list off and link to every challenge problem I have talked about on this blog.  If you are like me and like solving fun math problems, then you should check out the posts and try to solve the questions for yourself.  If you come up with a neat solution, feel free to share your solutions in the comments.  Here are the problems in the order that I blogged about them: A Fun Puzzle from Probability Analyzing an Unfair Game Counting Special Non-Descending Sequences Analyzing Randomly Descending Sequences Random Walk on a Complete Graph Pattern in Pascals Triangle Mathematics and Darts! ...

Artificial Neural Networks, and specifically deep neural networks have been gaining a lot of attention recently, and they are being used successfully across many disciplines. I first encountered neural networks a few years ago, but after hearing the term "backpropagation" and having no idea what it meant I feared that neural networks may be too complicated for me to understand. I made no attempts to truly understand them until recently, and have found that they are actually very easy to understand. I'm writing this blog post share my perspective on how to think about neural networks without jumping directly into the math.  This post is intended for beginners interested in machine learning using neural networks.  By the end of this blog post, you should be able to understand basics of neural networks enough to talk about them intelligently. And if you are so inclined, you can do a deeper dive into the mathematics that underlies the idea. In this blog post I will talk ...

Active learning is an interesting field in machine learning where the data is actively collected rather than passively observed.  That is, the learning algorithm has some influence over the data that is collected and used for learning.  The best example of this is Google AdWords, which uses active learning to serve ads to people in order to maximize click-through rate, profit, or some other objective function.  In this setting, the learning algorithm used by Google can choose which Ad to show me then it observes whether I clicked it or ignored it.  The learning algorithm will then update it's beliefs about the world based on this feedback so it can serve more relevant ads in the future. Since the learning algorithm doesn't know which types of ads are most relevant a priori, it must explore the space of ads to determine which ones produce the highest click-through rate.  However, it also needs to exploit it's current knowledge to maximize click-through rate. ...

Today I'm going to talk about a math problem whose answer is simultaneously simple and unintuitive.  Here is the problem statement: You have a urn that has $1$ red ball and $1$ blue ball.  You repeatedly remove one ball from the urn randomly, then put two balls of the same color back into the urn.  How does this system behave over time?  Specifically, what is the probability that at some point the urn will contain exactly $r$ red balls and $b$ blue balls? If you want to see my solution, go ahead and expand the solution tab.  Otherwise, you can try to figure it out for yourself.  Also, if you have other interesting questions you want to ask about this system, feel free to post them in the comments below. Show/Hide Solution Intuitively, this seems like a "rich get richer" problem", in that the long term behavior of the system depends on how "lucky" we are in the early stages (i.e., how many red and blue balls we pick).  For example, if we pick m...

One of the most common complaints about group projects in college is about work distribution: some people put in more work than others, and the people who put in more work do not think that is fair.  I've worked with many different groups in college, and I've been on both sides depending on the class and the project.  However, I don't actually mind putting in more work than other people when I enjoy the class and I think the project will provide a valuable learning experience.  By taking the lead, I end up understanding the project material much better than I would have otherwise.  However, when I don't care about the class as much, I tend to do less work.  So while I can't necessarily relate to other people who put in more work and complain about their teammates, I will offer some explanation as to why some people sit on the sidelines while other people take on the burden of doing the majority of the project. The first observation to make is that not everybod...

In this blog post, I am going to show why the work I did on  Day Three  is so important, and how using the strategy I outlined in that post can improve your odds of beating the streak by a factor of 5-10!  On day three, I analyzed the situations under which you should select a player who you think will get a hit, as opposed to not selecting that player, and instead maintaining your current streak until the next day.  In summary, I found that your decision should be guided by your current streak, the number of games left in the season, your confidence in the player (how likely is he to get a hit?), and the distribution of likelihoods across all games in the season.  After solving for the optimal strategy, I was able to approximate the probability of winning under that strategy by making some simplifying assumptions about the probability distribution of the best player getting a hit on a given day. I'm not going to get too deep into the math in this blog post, b...

I thought of this problem about two years ago and was going to send it out as the one of the weekly challenge problems for the ACM student chapter at UD, however I was unable to solve it when I first thought of it, and so I put it on the back-burner for a while.  Recently, I revisited it and made some progress on it, but was still unable to find a strategy that can solve it at all, let alone efficiently.  I am posting the problem to this blog in the hopes that you can help me figure it out by posting your ideas and code in the comments below.  Anyway, here is the problem: You are taking a quiz with $n$ true/false questions that you didn't study for, but you are allowed to retake the quiz as many times as you want. Every time you take the quiz, you are told how many questions you got correct, but not which questions were right and wrong.  Your final score is the number of answers you got correct on your last submission minus the number of times you retook the quiz. ...

Today I finished porting the content of my blog to this location.  It was a tedious process, but I think this is a more user friendly blogging platform than what I was using before, so it will pay off in the long run.  Blogger is a nice platform because they can host your blog for free, so the only thing I have to pay for to maintain this site is $12/year for the domain.  I'm not a web development expert, and the drag-and-drop nature of Blogger will allow me to produce content a little bit faster, and possibly nicer. Anyway, I decided to decouple my old website into two components: (1) a personal website which contains mostly static content and is more professional, and (2) this blog, which is more dynamic and informal.  However, there were some aspects of my old website that don't easily fit into either category, such as the pages about my academic interests, so I am going to slowly bring some that content into this blog and discard the rest of it. Here's a few...

In about a week, I will no longer have access to my old website at www.cis.udel.edu, so I am in the process of offloading the content of that website to other places on the web.  I am taking this as an opportunity to restructure my website a little bit, and have decided to try using a new blogging platform that will simplify the process of web development a little bit for me.  I'm hoping to transfer all of the blog posts to this new location this weekend, and then I'll figure out what to do with the rest of my website.  Anyway, this is just an initial post to let you know that my old website will no longer be maintained, and that this is the new location that I will use to post content.

My proudest accomplishment as an undergraduate student is the 400+ Project Euler problems I solved. In this blog post, I will do some data analysis on my progress over time, and talk about how I got to where I am today. In December 2014, I wrote a blog post about reaching my first Project Euler milestone: 200 problems solved. A lot has changed since then, and many of the techniques I used to reach 200 weren't very useful in getting to 400, as the problems became more challenging. The above plots show my progress over time. The first one simply shows the number of problems solved on a given date, and the second one breaks down my solved problems by difficulty (a recently added feature on Project Euler that tells you how challenging a problem is). I was over halfway done with undergrad when I reached 200 problems solved, so I never really thought I would get to 400 by the time I graduated, especially since the problems became significantly harder and my courses became more ...

With the recent high offensive production in the mlb, many people have amassed large streaks in the Beat the Streak contest.  The current leader has a streak of 41 games, which he got by picking exclusively red sox players.  Many other people have streaks in the high 30s, and I have a streak of 19 myself right now.  It seems like a lot more people have been getting longer streaks this year.  Some of this is probably due to the fact that more batters are getting hits this year than they have in the past, but it is probably also due to MLB.com's new pick selection system, which makes it easier than ever to make high quality picks using whatever strategy you want.  I would not be surprised if this is the year somebody wins.  If that's the case, this could be one of my last blog posts on this topic.     In this blog post, I am going to evaluate my current pick selection strategy  by testing it on data from 2015.  My data consists of a list ...

Today I'm going to be talking about the probabilistic classifier known as Naive Bayes, and a recent idea I came up with to improve it. My idea relies on the same assumptions that naive bayes does, but it finds different values for the conditional probabilities and class probabilities that describe the data better (or so I originally thought). In this blog post, I am going to quickly go through the traditional naive bayes setup, introduce my idea, then compare the two in terms of prediction quality. The Traditional Setup Let's assume we have a data set with \( N \) observations, where each observation has \( n \) attributes \( x_1, x_2, \dots, x_n \) and \( 1 \) class value \( C_k \). Naive bayes says that we can compute the probability of observing \( C_k \) given the attribute information by evaluating the following formula: $$ P(C_k | x_1, \dots, x_n) = \frac{ P(C_k) \prod_{i=1}^n P(x_i \mid C_k) }{P(x_1, \dots, x_n)} $$ where $$ P(x_1...

In this blog post, I will introduce an idea I recently came up with to predict the most likely players to get a hit in a given game based on situational factors such as opposing starter, opposing team, ballpark, and so on. I have not written much in this blog on this topic, although I did some work on this topic last fall which you can find here . In that work, I had the chance to explore a bunch of ideas that I had, but ultimately had to back up a few steps and rethink my approach. I think the ideas are still valid, and will continue refine them as time permits. A few weeks ago, I came up with a new approach that is completely different from my other approaches so far, and I will share it in the rest of this post. Defining the Problem Before we dive into the math, let's talk about what exactly we are trying to do. The end goal is to pick the player who is most likely to get a hit on a given day based on factors associated to the games for that day. Some of these facto...

The principle of inclusion exclusion is a very powerful idea that can be used to solve alot of problems that arise in combinatorics. In this blog post, I will show how it can be used to solve one problem in particular, and I will also provide a very elegant recursive implementation of it. Let's say we want to count the number of positive integers \( k \) that are less than or equal to \( m \) and relatively prime to \( n \). Using set theoretic notation, week seek to find the cardinality of the set \( \{ p \mid p \in \{ 1, 2, \dots, m \}, \gcd(n,p) == 1 \} \) where \( gcd \) is the greatest common divisor function. Let's denote the function that counts the cardinality of this set as \( f(n,m) \). Now that the problem has been defined, I will show how to solve it using brute force methods. We can map the mathematical definition of the problem to a haskell program very naturally using a list comprehension. f :: Int -> Int -> Int f n m = length [p | p &lt- [...