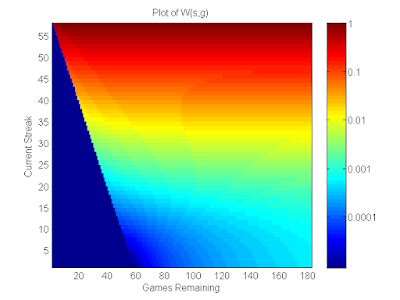
Biased Best-of-K Rock Paper Scissors
The topic of today's blog post is an interesting twist on the classical rock paper scissors game. Alice and Bob agree to play rock paper scissors (best of 1). If Alice loses, she loses gracefully and accepts defeat. If Bob loses, he will insist on playing best of 3. If he loses yet again, he will insist on playing best of 5, and so on and so forth. What is Alice's probability of winning this game if she is willing to agree to Bob's request $k$ times (best of up to $K=2k+1$)? Let's begin by working out the formula for $k=1$, which is perhaps the most realistic scenario. How much does Alice give up by agreeing to Bob's request once? The probability of Alice winning a given round is $1/2$, and same for Bob (a round is consists of a sequence of ties followed by exactly one non-tie). Here are the possible sequence of events, along with their probabilities, with A/B denoting that Alice/Bob wins the given round respectively. B - 0.5 - Bob wins in 1 turn AA -...