Ryan's Repository of Random Reflections

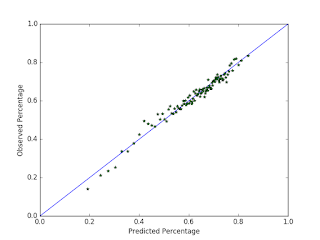
This semester I took the machine learning class at UMass, and for my final project I developed models for predicting characteristics of pitches based on the context that they were thrown in.  The context consists of relevant and available information known before the pitch is thrown, such as the identities of the batter and pitcher, the batter height and stance, the pitcher handedness, the current count, and many others.  In particular, I looked into modeling the distribution over pitch types and locations.  This problem is challenging primarily because for a particular context (a specific setting of the different features that make up the context), there is usually very little data available for pitches thrown in that context.  In general, for each context feature we include, we have to split up our data into $k$, groups where $k$ is the number of values that the context feature can take on (for batter stance it is $k=2$, for count it is $k=12$, etc).  Thus, de...

Artificial Neural Networks, and specifically deep neural networks have been gaining a lot of attention recently, and they are being used successfully across many disciplines. I first encountered neural networks a few years ago, but after hearing the term "backpropagation" and having no idea what it meant I feared that neural networks may be too complicated for me to understand. I made no attempts to truly understand them until recently, and have found that they are actually very easy to understand. I'm writing this blog post share my perspective on how to think about neural networks without jumping directly into the math.  This post is intended for beginners interested in machine learning using neural networks.  By the end of this blog post, you should be able to understand basics of neural networks enough to talk about them intelligently. And if you are so inclined, you can do a deeper dive into the mathematics that underlies the idea. In this blog post I will talk ...

Active learning is an interesting field in machine learning where the data is actively collected rather than passively observed.  That is, the learning algorithm has some influence over the data that is collected and used for learning.  The best example of this is Google AdWords, which uses active learning to serve ads to people in order to maximize click-through rate, profit, or some other objective function.  In this setting, the learning algorithm used by Google can choose which Ad to show me then it observes whether I clicked it or ignored it.  The learning algorithm will then update it's beliefs about the world based on this feedback so it can serve more relevant ads in the future. Since the learning algorithm doesn't know which types of ads are most relevant a priori, it must explore the space of ads to determine which ones produce the highest click-through rate.  However, it also needs to exploit it's current knowledge to maximize click-through rate. ...

With the recent high offensive production in the mlb, many people have amassed large streaks in the Beat the Streak contest.  The current leader has a streak of 41 games, which he got by picking exclusively red sox players.  Many other people have streaks in the high 30s, and I have a streak of 19 myself right now.  It seems like a lot more people have been getting longer streaks this year.  Some of this is probably due to the fact that more batters are getting hits this year than they have in the past, but it is probably also due to MLB.com's new pick selection system, which makes it easier than ever to make high quality picks using whatever strategy you want.  I would not be surprised if this is the year somebody wins.  If that's the case, this could be one of my last blog posts on this topic.     In this blog post, I am going to evaluate my current pick selection strategy  by testing it on data from 2015.  My data consists of a list ...

Today I'm going to be talking about the probabilistic classifier known as Naive Bayes, and a recent idea I came up with to improve it. My idea relies on the same assumptions that naive bayes does, but it finds different values for the conditional probabilities and class probabilities that describe the data better (or so I originally thought). In this blog post, I am going to quickly go through the traditional naive bayes setup, introduce my idea, then compare the two in terms of prediction quality. The Traditional Setup Let's assume we have a data set with \( N \) observations, where each observation has \( n \) attributes \( x_1, x_2, \dots, x_n \) and \( 1 \) class value \( C_k \). Naive bayes says that we can compute the probability of observing \( C_k \) given the attribute information by evaluating the following formula: $$ P(C_k | x_1, \dots, x_n) = \frac{ P(C_k) \prod_{i=1}^n P(x_i \mid C_k) }{P(x_1, \dots, x_n)} $$ where $$ P(x_1...