Beat the Streak: Day Six

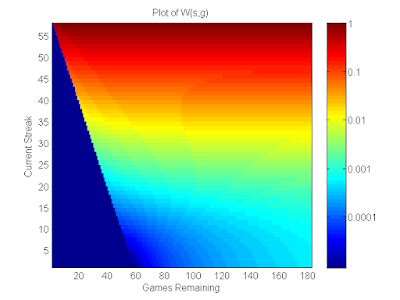
In this blog post, I am going to show why the work I did on Day Three is so important, and how using the strategy I outlined in that post can improve your odds of beating the streak by a factor of 5-10!  On day three, I analyzed the situations under which you should select a player who you think will get a hit, as opposed to not selecting that player, and instead maintaining your current streak until the next day.  In summary, I found that your decision should be guided by your current streak, the number of games left in the season, your confidence in the player (how likely is he to get a hit?), and the distribution of likelihoods across all games in the season.  After solving for the optimal strategy, I was able to approximate the probability of winning under that strategy by making some simplifying assumptions about the probability distribution of the best player getting a hit on a given day.

I'm not going to get too deep into the math in this blog post, but I want to give you a little bit of intuition behind the math that went into it.  Let's say that you are very good at making BTS picks, and so 80% of your picks end up getting hits.  Then the probability of correctly picking 57 times in a row is $ 0.8^{57} \approx 0.000003 $.  However, the probability of beating the streak is actually higher than this, because there are many 57-game windows that you could potentially beat the streak in.  The problem essentially reduces to: Consider a 183-length (# days in a season) bit string where each bit is 1 with probability 0.8 and 0 otherwise.  What is the probability that there are 57 1's in a row somewhere in the string?   This question can be answered by dynamic programming, and the probability is about $ 0.000078 $.  Since in beat the streak you can make up to two picks per day, we can approximate that scenario by simply doubling the length of our bit string.  Note that this is an approximation, and to solve it exactly would require a more complex model.  For a bit string of length 350 (about double, but not quite), the probability of having a 57-bit substring of all 1's would be about $ 0.00018 $ -- or 5620 to 1 odds.

If you are smart about when to take risks and when to be conservative by using the strategy I outlined on day three, you can improve your odds by a non-trivial amount.  In order to do that however, you need to have a way to assign a confident to the picks you make.  For example, if you have a method of selecting the best player every day and on average 80% of them end up getting a hit, you would have 5620 to 1 odds of winning using the simple strategy.  However, if you are able to assign a confidence to each of your picks, so that some of them have a better than 80% chance and other have a less than 80% chance of being successful, then you can wait for better opportunities when your streak is longer, but take more risks when your streak is shorter.  So even though your overall prediction accuracy is still 80%, by utilizing this strategy you can improve your odds of eventually obtaining a 57 games streak.

I wanted to get some concrete numbers to test this strategy, so I came up with an experiment where I calculated the probability of beating the streak under four situations:

1. The probability of getting a hit is $p$ every day.
2. The probability of getting a hit on a given day is sampled from a normal distribution with mean $p$ and standard deviation $0.01$ (68% of the time the probability will be within $[p-0.01,p+0.01]$).
3. The probability of getting a hit on a given day is sampled from a normal distribution with mean $p$ and standard deviation $0.02$ (68% of the time the probability will be within $[p-0.02,p+0.02]$).
4. The probability of getting a hit on a given day is sampled from a normal distribution with mean $p$ and standard deviation $0.03$ (68% of the time the probability will be within $[p-0.03,p+0.03]$).

I ran tests for $p$ ranging from $0.6$ to $0.9$.  My current models are around $0.73$ or $0.74$, but I am hoping to improve them to about $0.8$ by next season.  Below is a table summarizing the results.  The value in each cell is the odds of winning (e.g., for situation $1$ with $p=0.8$, the odds are 5620 to 1).

Odds Table
p	std=0.0	std=0.01	std=0.02	std=0.03
0.60	37500000000	14900000000	5460000000	1940000000
0.61	15000000000	6060000000	2270000000	824000000
0.62	6090000000	2510000000	960000000	355000000
0.63	2510000000	1050000000	411000000	155000000
0.64	1050000000	450000000	179000000	68700000
0.65	447000000	195000000	78800000	30900000
0.66	193000000	85400000	35200000	14000000
0.67	84200000	38000000	15900000	6480000
0.68	37300000	17100000	7310000	3020000
0.69	16800000	7820000	3400000	1430000
0.70	7620000	3620000	1600000	684000
0.71	3510000	1700000	762000	331000
0.72	1640000	804000	367000	162000
0.73	773000	386000	179000	80600
0.74	370000	188000	88600	40500
0.75	179000	92300	44300	20600
0.76	87500	45900	22400	10600
0.77	43300	23100	11500	5500
0.78	21700	11800	5930	2890
0.79	11000	6080	3110	1540
0.80	5620	3170	1650	831
0.81	2910	1670	886	454
0.82	1530	895	482	251
0.83	809	484	265	140
0.84	433	265	148	79.6
0.85	235	147	83.4	45.7
0.86	129	82.5	47.7	26.5
0.87	71.2	46.9	27.5	15.5
0.88	39.9	26.9	16.1	9.22
0.89	22.5	15.6	9.41	5.63
0.9	12.8	9.06	5.52	3.77

As you can probably see, this strategy significantly improves your odds of beating the streak, and the magnitude of the improvement increases with the standard deviation.  Without using the strategy, my odds of beating the streak would be about 370,000 to 1 ($p = 0.74$), but using this strategy I can improve them to 40,500 to 1 (assuming the standard deviation is $0.03$).  Similarly, if I ever improve my model to be 80% successful on average, I will be able to improve my odds from 5620 to 1 to 831 to 1 by using this strategy.

I showed in this post how you can non-trivially improve your odds of beating the streak by being smart about when to select 0, 1, or 2 players.  However, in order to use this strategy, you first need to be able to make well calibrated estimations about the likelihood that a particular player will get a hit in a given situation.  This is a very hard problem, and one that I have been struggling to answer for about a year now.  If you have any ideas on how to make well calibrated estimates, or if you would like to reproduce this work/ask any questions, feel free to reach out to me on Google+ or in the comments section below.