Deriving Perfect Strategy for Blackjack

In this blog post, I will discuss the algorithmic techniques needed to derive perfect strategy for the game of blackjack. Perfect strategy utilizes knowledge of the exact composition of cards remaining in the deck. No human can execute perfect strategy in practice since it requires keeping track of the count of 13 different cards simultaneously. It’s theoretically possible to use a technique like this to gain a slight advantage in online live dealer blackjack via software, and this strategy does provide a positive EV game, although as we will see later, the advantage is quite small. Nevertheless, it is quite an interesting algorithmic problem, and I had fun solving it. This will be the topic of this blog post. The Wizard of Odds has a great YouTube video showing how you can derive basic strategy for a simplified game with an infinite deck of cards. This is a great starting point for understanding this way of thinking. There are two main questions we ultimately want to answer: 1. Given the exact deck composition (number of 2s, 3s, …, Ks, As), a dealer up card, and player cards, what is the best action to take (highest EV)? 2. Given the exact deck composition, what is the EV of the next hand before the cards are dealt? The first question informs the optimal strategy in terms of actions taken, while the second question informs our betting system (bet large when EV is positive, bet small or none when EV is negative). We will focus on answering question 1 first. With a complete solution to question 1, it is relatively straightforward to answer question 2. In this blog post, we use the term EV extensively, which is the expected value of the hand in a given context under optimal play, assuming a unit sized bet.  

High-Level Approach

To answer question 1, we need to be able to compute the EV for every possible action in a given context. Here, I am simply using the term context to refer to all the information known to the player at the given time, including the deck composition, the dealer up card, and the players hole cards. The possible actions are: Hit (H), Stand (S), Double (D), Split (P), and Surrender (R). Depending on the player hole cards, only some of these options may be available (i.e., splitting, doubling and surrendering is only possible when the player has 2 hole cards, and split is only possible when those two cards are equal). 

EV for standing 

We will begin with a calculation to compute the EV of standing in a given context. To calculate the EV, we use a brute force approach. We enumerate all possible sequences of cards the dealer could draw before the rules of the game say they should stop drawing (i.e., they have hard 17 + or soft 18+). For each possible sequence, we will calculate its probability as well as the outcome (+1 if dealer busts or stands on total less than ours, -1 if dealer stands on total greater than ours, and 0 if dealers total matches ours). Summing up over all possible sequences yields the desired EV. While this may seem like a very inefficient approach, it’s actually not too bad: there are #### total possible dealer sequences that we have to iterate through, and with a careful implementation this is very quick. 

EV for hitting 

Next, we will discuss how to calculate the EV for hitting in a given context. Note that if we decide to hit there are two possibilities: (1) we bust, losing immediately and (2) we don’t bust, and we have a choice to either hit or stand in the new context. The EV of (1) is clearly -1 and the EV of (2) is max(EV_{stand}(new context), EV_{hit}(new context)). Thus, to calculate the EV in the current context, we will: (1) enumerate over the 13 possible cards we could draw, (2) compute the probability of drawing that card from the context, (3) compute the EV in the new context, and (4) sum over the product of (2) and (3) above to get the final EV of hitting in the current context. Note that EV_{hit} is defined recursively: in order to calculate it for a given context, we need to know its value for other contexts. Fortunately, the recursion always terminates since the new context always contains a deck with one less card, and the player total is closer to busting. (When the player total exceeds 21, the EV is -1).  

EV for doubling 

To calculate the EV of doubling in a given context, it suffices to (1) enumerate the 13 cards we might be dealt, (2) compute the probability of drawing that card based on the current deck composition, (3) compute the EV_{stand}(new context), and (4) compute the EV of doubling as two times the sum over the product of (2) and (3) above.  Unlike for hitting, there is no recursion here.  As long as we know EV_{stand} for all contexts, we can calculate EV_{double} directly.

EV for splitting

Calculating the EV of splitting is tricky, since the player has to play out two hands, and the outcome of the first hand affects the deck composition of the second hand.  This is difficult/expensive to take into account algorithmically.  Therefore, as a standard approximation, we will calculate the EV for one of the hands, and just multiply that EV by two to estimate the EV of splitting.  Additionally, for simplicity, we will assume that a player is only allowed to split once, even though it is common to allow splitting up to four times.  After a player splits, they are dealt another card, at which point they can either Double, Hit, or Stand.  To calculate the EV of splitting we will (1) enumerate over the 13 cards we might be dealt, (2) compute the probability of drawing that card based on the deck composition, (3) compute max(EV_{Double}(new context), EV_{Hit}(new context), EV_{Stand}(new context)}, and (4) sum up over the product of (2) and (3), and multiply that result by two.  Assuming EV_{Double}, EV_{Hit}, and EV_{Stand} have already been computed for all possible contexts, this computation can be done directly.

EV for surrendering

The EV of surrendering is always -0.5.  

Choosing the best action

In a given context, choosing the best action is as simple as computing the EV for all legal actions in that context, and picking the action with the maximum EV.  In a standard full 8 deck shoe, the best action according to this approach will essentially resemble basic strategy exactly.  However, more interesting things happen with more exotic deck compositions that may materialize as a shoe plays out.  

Calculating the EV an undealt hand

Computing the EV of an undealt hand is important to determine bet sizes: with positive EV, we have the advantage under optimal play, and with negative EV, the house does.  When we compute the best action for a given context, we will also store the EV of that action in a lookup table.  We will use this lookup table to calculate the EV of an undealt hand.  Specifically, we (1) enumerate over all 13 x 13 x 13 = 2197 cards that could be dealt to the player and the dealer (2) calculate the probability of being dealt those cards based on the deck composition and (3) calculate the EV of the resulting context by utilizing the aforementioned lookup table.  

Analyzing the time and space complexity

The input to the program is a single context, which includes the deck composition along with a list of cards dealt so far.  How much time does it take to calculate the expected values using the approach described above?  First note that we can calculate exactly the number of possible deck compositions that can be realized by playing out a hand with a given deck composition.  This can be done via a brute force method that deals out all possible hands.  In total there are at most 35946 possible deck compositions that are realizable during the dealing of a hand.  Depending on the deck composition, there may be fewer possible hands since e.g., we could run out of a certain card during the dealing of a hand.  

In addition to the deck composition, the context we need to keep track of includes the current player total (21 possibilities) as well as the dealer upcard (10 possibilities, if you group face cards together).  Thus, the size of our lookup tables for EV_{Hit}, EV_{Stand}, EV_{Double}, and EV_{Split} is $ 35946 * 21 * 11 = 7,548,660$.  These are very large lookup tables, and my initial python implementation of this algorithm was painfully slow.  However, I iterated on the code and implemented it in C++ and can now compute the expected value and best action for any context in under a second (although this depends on the hardware being run on).

Simulations

To test how good this strategy works, I implemented a blackjack simulator that deals out  hands from an 8 deck shoe (standard in online live dealer blackjack) until there are fewer than 52 cards remaining, in which case I reshuffle and start a new shoe.  For each hand, I call into the C++ API to determine the EV and best action for each context.  All in all, I simulated about 1.3 million hands.  

Sanity Check

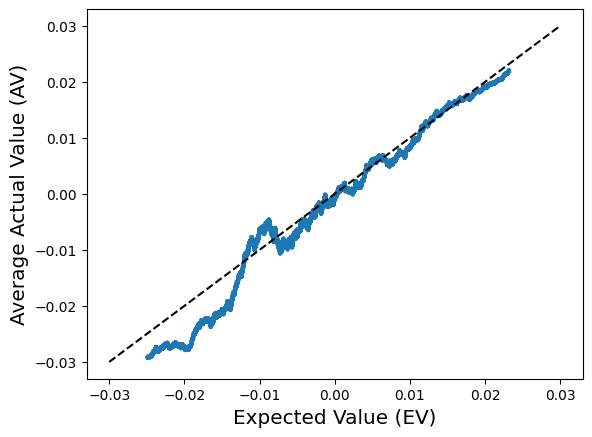
I begin by first checking that the EV’s that my program calculates match up well with the actual values observed.  To do this, I sort my data by EV, and computing the rolling mean of both EV and AV for 200K hands.  The plot below shows that EV predicts AV well, which gives me confidence that there are no bugs in the implementation.  

For each hand dealt, I keep track of the deck penetration (or the fraction of the deck that has already been dealt).  I will use this to filter the data, as in online live dealer blackjack, the deck is reshuffled at about 50% deck penetration.  Next, I look at the distribution of EV over the course of dealing out 4 decks from an 8 deck shoe.  The plot below shows that the EV is centered around -0.00547, or equivalently a house edge of 0.547%.  20% of deck compositions are positive EV, while 80% are negative EV.  Additionally, only 3.96% of hands have an EV greater than 0.01.  

For sake of the visualization, in the plot below I also show what happens if we deal down to 1 deck, which from my understanding is more common in brick and mortar casinos.  As we can see, the average EV is still centered around -0.0054, but now there are more positive EV deck compositions and  larger player advantages.  Specifically, 31% of deck compositions are positive EV and 13.7% of them have EV greater than 0.01.  

How profitible is this approach? 

We are finally ready to answer the question that has been asked over and over again: can you count cards in online live dealer blackjack?  The answer is Yes, and you will have a positive EV game.  However, even with the perfect composition-dependent optimal strategy described in this blog post, it requires playing a lot more hands with a much larger bankroll/bet spread than you could get away with by going to a brick and mortar casino.  Moreover, the player advantages are smaller (rarely exceeding 1%), which increases variance and hence risk of ruin.  

Suppose we use the following betting system:

• Bet 0 if EV <= 0
• Bet EV*10000 if EV > 0 (e.g., a 100 dollar bet at EV=0.01)

i.e., we bet in proportion to our advantage.  The following plots shows how this strategy would pan out in our simulation over 800K hands with deck penetration >= 50%.  The plot shows an expected profit of about 100,000 dollars and an actual profit of 60,000 dollars.  

That is pretty good, but if we change the setup and require a min bet of 10 dollars even at negative EV, this reduces our overall EV to 50,000 dollars and drastically increases our variance, even bringing our AV to negative, as shown below:

This suggests that a 10 to 1 bet spread is not sufficient in this setting, and more aggressive bet spreads are necessary to mitigate the negative EV settings.  In addition, even if one could play 100 hands per hour, and we could play 24 hours a day it would take nearly a year to play 800K hands, making this idea much less appealing. 

Conclusion

Blackjack and advantage play is a topic that I have found pretty interesting, and I had fun thinking about this problem and developing an efficient algorithm for computing expected values and composition-dependent optimal strategy.  If you would like to reproduce the results in this blog post, I have uploaded the C++ API, python simulation code, and plotting notebook to GitHub.