Pattern in Pascal's Triangle
- Get link
- X
- Other Apps
Pascal's Triangle is a triangular array of binomial coefficients, and it often arises in counting problems. In this blog post, I will present a problem that is related to Pascal's triangle and in solving it, I will derive an interesting relationship in Pascal's Triangle that you probably didn't know about.
If you randomly walk down \( n \) rows of Pascal's Triangle by going down-left or down-right at each step, what is the expected value of the number that you finish on?
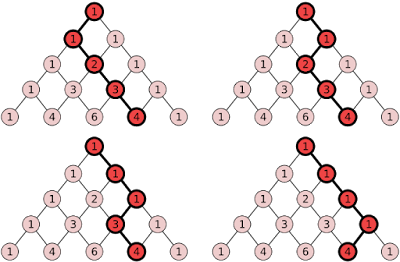
For example, if \( n = 4 \), then here are a few possible walks (that all happen to end at 4):
$$
E(X) = \frac{1}{2^n} \sum_{k=0}^{n} {n \choose k}^2
$$ While this is an acceptable answer, and we can readily compute this with the help of a computer, let's make some further simplifications. In doing this, I will derive an interesting pattern that you probably haven't seen before.
Let \( S(n) = \sum_{k=0}^{n} {n \choose k}^2 \). Clearly, \( S(1) = 2, S(2) = 6, S(3) = 20, \) and \( S(4) = 70 \). Do you see a pattern? If you expand Pascal's triangle out a few more rows, you will probably notice that \( S(n) \) is given by the middle element of the even numbered rows. More formally, \( S(n) = {2n \choose n} \).
$$
\sum_{k=0}^{n} {n \choose k}^2 = {2n \choose n}
$$ One way to show this summation holds is to use induction, but I will merely show the key insight on why this equality holds, and will not bother to make it rigorous for the sake of simplicity. Using the identity
$$
{n \choose k} = {n-1 \choose k-1} + {n-1 \choose k}
$$ we can readily see that
$$
{2n \choose n} = {2n-1 \choose n-1} + {2n-1 \choose n}
$$ Repeatedly applying the identity to each term, we can see
$$
\begin{split}
{2n \choose n} &= {2n-2 \choose n-2} +
2 {2n-2 \choose n-1} +
{2n-2 \choose n}\\
{2n \choose n} &= {2n-3 \choose n-3} +
3 {2n-3 \choose n-2} +
3 {2n-3 \choose n-1} +
{2n-3 \choose n} \\
{2n \choose n} &= {2n-4 \choose n-4} +
4 {2n-4 \choose n-3} +
6 {2n-4 \choose n-2} +
4 {2n-4 \choose n-1} +
{2n-4 \choose n} \\
& \vdots \\
{2n \choose n} & = \sum_{k=0}^{n} {n \choose k}^2
\end{split}
$$ While that method works, there is actually a simple interpretation for why this equality holds. Recall that \( n \choose k \) counts the number of ways to pick \( k \) labeled balls from a urn containing \( n \). Thus, \( {2n \choose n} \) is the number of ways to pick \( n \) balls from a urn with \( 2n \). Consider this methodology:
$$
{2n \choose n} = \sum_{k=0}^{n} {n \choose k} {n \choose n-k}
$$ Noticing that \( {n \choose k} = {n \choose n-k} \), we can get back to the original equality
$$
{2n \choose n} = \sum_{k=0}^{n} {n \choose k}^2
$$ The answer to the original question is
$$
\boxed { E(X) = \frac{1}{2^n} {2n \choose n} }
$$
If you randomly walk down \( n \) rows of Pascal's Triangle by going down-left or down-right at each step, what is the expected value of the number that you finish on?
For example, if \( n = 4 \), then here are a few possible walks (that all happen to end at 4):
Solution
The first thing to notice is that the number of ways to walk to any cell in the triangle, is the value of the cell itself! That's because you can get to any cell by going through either it's left parent or it's right parent, and by the way this triangle is constructed, we know that the value of each cell is the sum of the values of it's two parents. Thus, there are \( n \choose 0 \) ways to get to \( n \choose 0 \), \( n \choose 1 \) ways to get to \( n \choose 1 \), etc. Further, there are a total of \( 2^n \) possible paths because you can choose between two options (namely down-left and down-right) \( n \) times. If we let \( X \) be the value that we finish on, then the desired expectation is given by$$
E(X) = \frac{1}{2^n} \sum_{k=0}^{n} {n \choose k}^2
$$ While this is an acceptable answer, and we can readily compute this with the help of a computer, let's make some further simplifications. In doing this, I will derive an interesting pattern that you probably haven't seen before.
Let \( S(n) = \sum_{k=0}^{n} {n \choose k}^2 \). Clearly, \( S(1) = 2, S(2) = 6, S(3) = 20, \) and \( S(4) = 70 \). Do you see a pattern? If you expand Pascal's triangle out a few more rows, you will probably notice that \( S(n) \) is given by the middle element of the even numbered rows. More formally, \( S(n) = {2n \choose n} \).
$$
\sum_{k=0}^{n} {n \choose k}^2 = {2n \choose n}
$$ One way to show this summation holds is to use induction, but I will merely show the key insight on why this equality holds, and will not bother to make it rigorous for the sake of simplicity. Using the identity
$$
{n \choose k} = {n-1 \choose k-1} + {n-1 \choose k}
$$ we can readily see that
$$
{2n \choose n} = {2n-1 \choose n-1} + {2n-1 \choose n}
$$ Repeatedly applying the identity to each term, we can see
$$
\begin{split}
{2n \choose n} &= {2n-2 \choose n-2} +
2 {2n-2 \choose n-1} +
{2n-2 \choose n}\\
{2n \choose n} &= {2n-3 \choose n-3} +
3 {2n-3 \choose n-2} +
3 {2n-3 \choose n-1} +
{2n-3 \choose n} \\
{2n \choose n} &= {2n-4 \choose n-4} +
4 {2n-4 \choose n-3} +
6 {2n-4 \choose n-2} +
4 {2n-4 \choose n-1} +
{2n-4 \choose n} \\
& \vdots \\
{2n \choose n} & = \sum_{k=0}^{n} {n \choose k}^2
\end{split}
$$ While that method works, there is actually a simple interpretation for why this equality holds. Recall that \( n \choose k \) counts the number of ways to pick \( k \) labeled balls from a urn containing \( n \). Thus, \( {2n \choose n} \) is the number of ways to pick \( n \) balls from a urn with \( 2n \). Consider this methodology:
- Partition the balls into two urns, each containing n. If we want n balls total, then we can take up to n from urn 1, and the rest from urn 2.
- We can take \(0\) balls from urn 1 and \(n\) from urn 2 for a total of $ {n \choose 0} {n \choose n} $
- We can take \(1\) ball from urn 1 and \(n-1\) from urn 2 for a total of $ {n \choose 1} {n \choose n-1} $
- We can take \(2\) balls from urn 1 and \(n-2\) from urn 2 for a total of $ {n \choose 2} {n \choose n-2} $
- We can take \(3\) balls from urn 1 and \(n-3\) from urn 2 for a total of $ {n \choose 3} {n \choose n-3} $
- We can do this until we capture all possibilities
$$
{2n \choose n} = \sum_{k=0}^{n} {n \choose k} {n \choose n-k}
$$ Noticing that \( {n \choose k} = {n \choose n-k} \), we can get back to the original equality
$$
{2n \choose n} = \sum_{k=0}^{n} {n \choose k}^2
$$ The answer to the original question is
$$
\boxed { E(X) = \frac{1}{2^n} {2n \choose n} }
$$
- Get link
- X
- Other Apps

Comments
Post a Comment