Beat the Streak Day 17: Coordinated Pick Selection

My current best pick selection model for BTS achieves roughly 78% accuracy.  Looking at the table from Day Six, we can see that with an optimal pick selection strategy, my odds of beating the streak are roughly 11,800 to 1, or roughly a 0.01% chance of winning.  In this blog post, I will explore methods for boosting this probability by coordinating picks across multiple accounts (e.g., friends, family, other BTS enthusiasts, etc.)

To the non-mathematically inclined, one might think that with $k$ accounts our probability of beating the streak as a group would simply multiply by $k$.  This simple formula is not correct, however, although it is an upper bound.  If each account has a probability $p$ of beating the streak, and there are $k$ accounts, the probability that at least one account beats the streak would be $1 - (1 - p)^k$ if we (incorrectly) assume independence between accounts.  For small $p$ and small $k$, this is pretty close to to the upper bound.  For example, with $p=0.0001$ and $k=2$, we have $ 1 - (1-p)^k = 0.00019999$ which is very close to double the probability.  With an even better model where $p=0.001$ and more accounts like $k=100$, we could get this probability up to $ 1 - (1-p)^k = 0.0952 $, which is actually not all that unlikely.  

Unfortunately, even this calculation is not correct, since it incorrectly assumes independence between accounts.  In practice, accounts have to select from the same pool of players, and there will definitely be overlap between the players selected by multiple accounts, which breaks the independence assumption.  The number we calculated under an independence assumption is the hypothetical best-case scenario.  In this blog post, we will see how close to this hypothetical best-case scenario we can get under some simplifying assumptions?  In order to answer this question, it is useful to consider the following problem abstraction:

Suppose we have a pool of $t$ picks each of which have a probability $p=0.8$ of getting a hit each day.  Suppose we have $k$ BTS players selecting players from this pool on each day.  

• Question 1: How should these players coordinate their picks to maximize the probability of beating the streak as a group?  

• Question 2: What is that probability, how does it depend on $t$ and $k$, and how close to the upper bound assuming independence $t \geq k$)?

Note that this problem abstraction is a simplified version of BTS, and does not take into account every aspect of the game, for example

• The pool and associated hit probabilities change from game to game.  [This aspect of the problem was analyzed in Day Three and Day Six.]
• The picks in the pool have different hit probabilities (they are not all $0.8$).  E.g., the best pick might have a probability of $0.8$ and the second best might have a probability of $0.79$, etc.
• We assume that each BTS player can select a single player each day, rather than two players allowed by the double down rule.  To approximate the effect of the double down rule, we assume the season has twice the number of days ~364.  

Simulations

We will attack the above problem by simulation for sake of simplicity.  In order to run the simulation, we first need to specify how the $k$ BTS players will select picks from the pool of size $t$.  I propose a simple strategy where each BTS player will simply select a pick at random from the pool.  As we will see below, this simple strategy works pretty well.  

Analyzing the effect of pool size

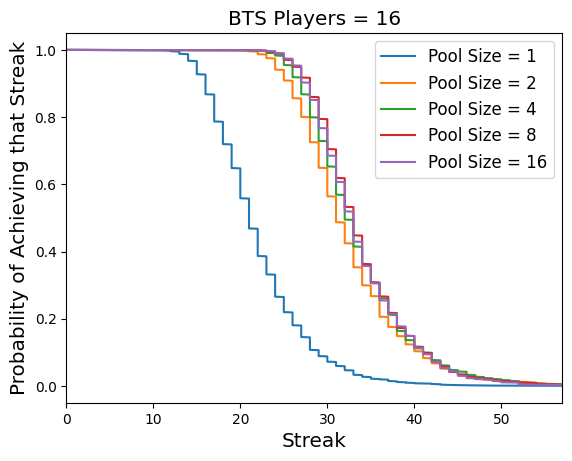
We will begin by analyzing the effect of the pool size for a fixed number of BTS players.  With $t=1$, all players have to make the same pick each day, and hence there is nothing to gain by increasing the number of players.  If we set $t=k$ we can achieve perfect independence by having every BTS player choose a different pick.  However, it would be hard to identify $k$ high-probability picks for large $k$.  Fortunately, the plot below shows that we can realize most of the gain by setting $t=2$, and going beyond that gives only marginal improvements.

Analyzing the effect of the number of BTS players

Next, we will analyze the effect of changing the number of players with a fixed pool size of $t=2$.  In the first plot below, we vary the number of players from $1$ to $16$, and see consistent and predictable improvements as we increase $k$.  Specifically, each time we double $k$, the average best streak increases by $3$.  Moreover, the probability of beating the streak approximately doubles each time as well.  Note that the table and plot below are the result of a simulation, and do not represent exact probabilities and expected values, but rather approximations from ~4000 trials.  

BTS Players	1	2	4	8	16
Average Group Best Streak	21.8	24.8	27.6	30.2	32.8
Probability of Beating the Streak	0.000244	0.000488	0.000732	0.001953	0.00244

In the next plot, I will zoom on on the 16 player line, and compare it to the hypothetical best-case scenario where each BTS player makes different/independent picks of equal quality.  We plot the y-axis on a log scale so we can better see what happens at the extreme where the streak approaches 57.  We see that the heuristic approach we take of randomizing the pick selection from a pool of size 2 is nearly as good as the hypothetical best-case scenario where each BTS player is completely independent.  This is great news.  Note that the "upper bound" is not always a true upper bound in this plot, but this is easily explained by the fact that this plot was constructed from simulations rather than closed form expressions.  

Conclusion

I initially thought this problem would be harder, and indeed an exact solution to this problem would require more heavy machinery.  However, the simple heuristic I proposed of randomizing the pick assignment seemed to work quite well, and hence solving this problem exactly does not seem worth the effort, and my time will be better spent improving my models. 

To summarize, I found that (somewhat surprisingly) the correlation between picks does not impact our probability of beating the streak as a group as much as I initially conjectured.  Moreover, advanced coordination is not even necessary, as each BTS player can follow a simple (random) pick selection strategy.  Additionally, only two high-quality picks must be identified each day to realize most of the benefit of group coordination.  Finally, the probability of beating the streak as a group increases predictably with increases to the group size, with each doubling of group size approximately translating into double the probability of beating the streak.  

If you would like to reproduce the plots in the blog post, or see how they were generated, you can check out this colab notebook.