Beat the Streak: Day Seven

-
In this blog post, I discuss questions of the form: “Does batter X perform better at home or away?  At day or night?  Against lefties or righties? On Friday or Monday?”  What I found was a little bit surprising.  

Take for example the batter Daniel Murphy.  When you look at his data from 2011 - 2017, you will see that he got a hit in 29.85% of 1424 plate appearances during day games and he got a hit in 26.97% of 2673 plate appearances during night games.  This is a pretty meaningful difference, but is it statistically significant?  In other words, could this difference be explained purely by chance?  To answer this question, we can perform a chi squared test under the null hypothesis that the true probabilities are the same.  When we do this we get a chi squared value of 3.35 and a corresponding p value of 0.067.  Thus, we can reject the null hypothesis that the true underlying probabilities are the same at the 90% confidence level.  This is pretty convincing evidence that the day/night split really matters, at least for Daniel Murphy, right?

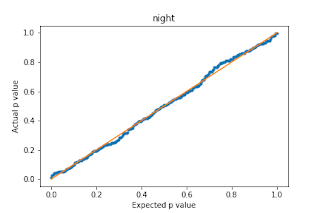
Wrong.  When we repeat this analysis for other batters we find that the difference is not usually statistically significant.  That is to be expected however, so perhaps it matters for some batters but not for others?  To answer this question we should look at the p value for all batters with enough data to satisfy the assumptions of the chi squared test (at least 5 hits at both day and night).  If the null hypothesis is true that the underlying hit probability is the same at day and night for all batters, then we still expect the 10% of the p-values to be less than 10% purely by chance.  More generally, we expect q% of p-values to be less than q% purely by chance for all q.  Thus, if we compute and sort the p-values for all $n$ batters, we expect batter $I$ to have a p-value around $i/n$ under the null hypothesis.  Here is the plot:
Because the true p-value appears along the main diagonal, this is very good evidence in support of the null hypothesis, and we are thus unable to reject it.  We conclude that day / night does not affect the hit probability.  We can repeat this analysis for other possible explanatory features such as weekday, month, pitcher handedness (p_throws), inning, order in lineup, home/away, ballpark, and year.  When we do so, we get the following plots:



When the blue points fall below the main diagonal, that is evidence that the feature is important and the null hypothesis can probably be rejected. The further below the main diagonal it is, the stronger the evidence.  We conclude that weekday, month, and order don’t really impact the hit probability, but p_throws, inning, home, ballpark, and year do.  It is a little surprising that the inning matters — perhaps this is because starting pitchers become more hittable as they get tired or relief pitchers are stronger/weaker than starters on average?  The year also matters, which is expected and indicates that (some) batters performance really does change from year to year, and the differences aren’t due purely to chance.  

The other thing to note about these plots is that for most batters, there is not statistically significant evidence to reject the null hypothesis, which is an indication that the impact of the features is small.  However, as a whole (using all batters), there is enough evidence to reject the null hypothesis.  If we wanted to be rigorous, we would have to calculate how far below the main diagonal we’d need to be to reject the null hypothesis.  Perhaps we could use area under the curve as a test-statistic?  I’m not sure, if you have any ideas feel free to comment below.

Comments

Post a Comment

Popular posts from this blog

Optimal Strategy for Farkle Dice

-
In this post, I will discuss my findings in terms of an optimal strategy for Farkle , which is a dice game of chance.  If you are unfamiliar with the game, I encourage you to skim the linked article so that you can better understand this blog post.  All of my findings are based on sound mathematical methods and a computer program was used to determine the optimal strategy.  Before I begin, let me first state the value of different dice rolls I assumed while developing the strategy. Each 1: 100 points Each 5: 50 points 3 1's: 1000 points 3 2's: 200 points ... 3 6's: 600 points 4 1's: 2000 points ... 4 6's 1200 points 5 1's 3000 points ... 5 6's 1800 points Straight 1-6 1500 points 3 Pairs (e.g., 22 33 44): 750 points Everything else is considered to be a Farkle (0 points). There are many variants to Farkle, but I like to play by this set of rules. The "game state" of Farkle roll can roughly be characterized by 2 values: the curre
Read more

Markov Chains and Expected Value

-
A few weeks ago, I was using a Markov Chain as a model for a Project Euler problem, and I learned about how to use the transition matrix to find the expected number of steps to reach a certain state. In this post, I will derive the linear system that will help answer that question, and will work out specific an example using a 1-dimensional random walk as the model. Terminology Before I begin the derivation, let me define some terms. The transition matrix is an \( n \) by \( n \) matrix that describes how you can move from one state to the next. The rows of the transition matrix must always sum to 1. States can either be transient or absorbing . An absorbing state is one that cannot be left once reached (it transitions to itself with probability 1). A transient state is a state that is not an absorbing state. In many problems, it is of general interest to compute the expected number of steps to reach an absorbing state (from some start state). Derivation  Let \( p_
Read more

Automatically Finding Recurrence Relations from Integer Sequences

-
In a lot of the recreational math and computer science problems I solve, I try to derive a recurrence relation that describes the situation. These recurrence relations pop up pretty often in counting problems (how many ways can you tile a 2xn grid with 2x1 tiles?) In some cases, I am unable to derive a recurrence relation directly from the problem statement, but still suspect that there exists some recurrence relation. In these cases, I end up solving the problem usin g brute force methods for small input sizes and analyzing/extrapolating the pattern. However, when the relation is obscure, it becomes hard to find. In order to make this process easier in the future, I created a program that can automatically find recurrence relations for arbitrary integer sequences. To use it, simply type in the first few terms of a sequence you are interested in, and it will try to find a recurrence relation for that sequence. There are some constraints on the allowable inputs/outputs which I di
Read more