A Simple Derivation of the Quadratic Formula

-
In this blog post, I will talk about the famous quadratic formula - a formula for finding the zero(s) of a polynomial equation of degree 2. I first learned this equation in Algebra, but I had always thought of it as a mathematical truth, without actually knowing how it came to be or why it's justified. Now, I have the tools to show that it's correct and to actually derive it using simple algebra.


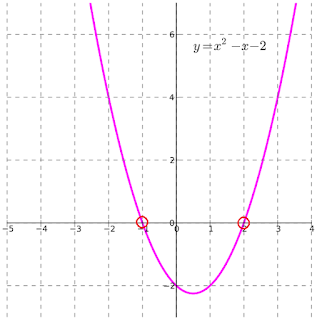
The quadratic formula is a formula used to solve for the zero(s) an arbitrary polynomial in the form $y = ax^2+bx+c$.  Here it is in it's standard form:

$$ x = \frac{-b \pm \sqrt{b^2 - 4 a c}}{2 a} $$

My proof of this formula relies on an algebraic trick known as completing the square, which is another useful technique to solving equations of this form. While I personally prefer the completing the square method because it's faster, many people prefer using the quadratic formula because it doesn't require much thought or intuition; it's straight plug-and-chug. Here is my proof:

Comments

Post a Comment

Popular posts from this blog

Optimal Strategy for Farkle Dice

-
In this post, I will discuss my findings in terms of an optimal strategy for Farkle , which is a dice game of chance.  If you are unfamiliar with the game, I encourage you to skim the linked article so that you can better understand this blog post.  All of my findings are based on sound mathematical methods and a computer program was used to determine the optimal strategy.  Before I begin, let me first state the value of different dice rolls I assumed while developing the strategy. Each 1: 100 points Each 5: 50 points 3 1's: 1000 points 3 2's: 200 points ... 3 6's: 600 points 4 1's: 2000 points ... 4 6's 1200 points 5 1's 3000 points ... 5 6's 1800 points Straight 1-6 1500 points 3 Pairs (e.g., 22 33 44): 750 points Everything else is considered to be a Farkle (0 points). There are many variants to Farkle, but I like to play by this set of rules. The "game state" of Farkle roll can roughly be characterized by 2 values: the curre
Read more

Markov Chains and Expected Value

-
A few weeks ago, I was using a Markov Chain as a model for a Project Euler problem, and I learned about how to use the transition matrix to find the expected number of steps to reach a certain state. In this post, I will derive the linear system that will help answer that question, and will work out specific an example using a 1-dimensional random walk as the model. Terminology Before I begin the derivation, let me define some terms. The transition matrix is an \( n \) by \( n \) matrix that describes how you can move from one state to the next. The rows of the transition matrix must always sum to 1. States can either be transient or absorbing . An absorbing state is one that cannot be left once reached (it transitions to itself with probability 1). A transient state is a state that is not an absorbing state. In many problems, it is of general interest to compute the expected number of steps to reach an absorbing state (from some start state). Derivation  Let \( p_
Read more

Automatically Finding Recurrence Relations from Integer Sequences

-
In a lot of the recreational math and computer science problems I solve, I try to derive a recurrence relation that describes the situation. These recurrence relations pop up pretty often in counting problems (how many ways can you tile a 2xn grid with 2x1 tiles?) In some cases, I am unable to derive a recurrence relation directly from the problem statement, but still suspect that there exists some recurrence relation. In these cases, I end up solving the problem usin g brute force methods for small input sizes and analyzing/extrapolating the pattern. However, when the relation is obscure, it becomes hard to find. In order to make this process easier in the future, I created a program that can automatically find recurrence relations for arbitrary integer sequences. To use it, simply type in the first few terms of a sequence you are interested in, and it will try to find a recurrence relation for that sequence. There are some constraints on the allowable inputs/outputs which I di
Read more