Tail Bounds on the Sum of Half Normal Random Variables
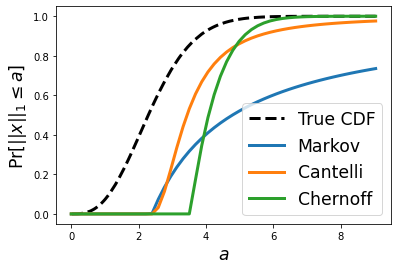
Let $ x \sim \mathcal{N}(0, \sigma^2)^n $ be a vector of $ n $ i.i.d normal random variables. We wish to provide a high probability tail bound on the $L_1$ norm of $x$, that is: $$ Pr[|| x ||_1 \geq a] \leq f(a) $$ Note that the term on the left is called a "tail probability" because it captures the probability mass in the tail of the distribution (i.e., values exceeding a). This type of problem arises when we wish to claim that the probability is small for a given random variable to be large. The tail probability above is closely related to the CDF of the random variable $ || x ||_1 $: it is exactly $ 1 - Pr[|| x ||_1 \leq a] $. Unfortunately, the CDF of this random variable does not appear to have a clean closed form expression, and for that reason, we wish to find a reasonably clean and tight bound on it instead. In this blog post, we will explore, utilize, and compare the Markov inequality , the one-sided Chebyshev inequality , and the Chernoff bound t...