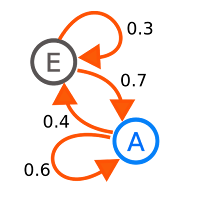
Solving Problems with Dynamic Programming
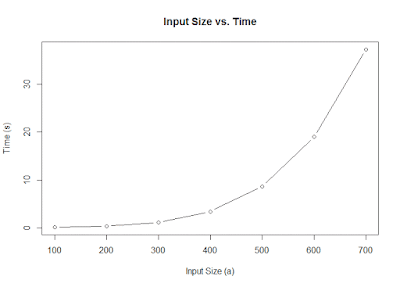
Dynamic Programming is a programming technique used to solve large, complex problems that have overlapping sub-problems. It does this by computing each sub-problem only once, ensuring non-exponential behavior. It differs from memoization (no, that's not a typo) in that instead of computing the result of a function then storing it in a cache, it instead generates a certain result before calculating any other result that relies on it. Dynamic Programming problems often require a different way of thinking than typical problems. Most often, dynamic programming becomes useful when you want to reverse engineer a tree recursive function. By that I mean you want to start of with the base case(s), then use those to generate the next few cases, and repeat this process until all points of interest have been calculated. Most often, at least in imperative languages, these dynamic programming algorithms are iterative, meaning they don't have recursive calls. That being said, it's still...